Neue Ans?tze für die mehrdimensionale Konvexifizierung inelastischer Variationsmodelle für Bruchph?nomene

PI: Prof. Dr. Daniel Peterseim

?

Die Modellierung und Simulation von Sch?digung ist von grundlegendem ingenieurwissenschaftlichen Interesse. Auf der Makroskala ?u?ern sich Sch?digungen durch Stress- und Strain-Softening Effekte sowie Bruch in Folge von Rissausbreitung. Bei Erreichen bestimmter mikroskopischer Sch?digungsgrade sto?en klassische Kontinuumssch?digungsmodelle auf einen Verlust der Konvexit?t der zugeh?rigen inkrementellen Variationsformulierung, was ihre Anwendbarkeit grundlegend einschr?nkt.
Relaxationssans?tze, die auf Konvexifizierung basieren, liefern Modelle welche netzunabh?ngige L?sungen garantieren und homogenisierte Mikrostrukturen beschreiben. Obwohl in jüngster Zeit bedeutende Fortschritte in Bezug auf effiziente numerische Konvexifizierungsverfahren gemacht wurden, sind Berechnungen für komplexe Strukturen in drei Dimensionen derzeit nicht praktikabel. Eines der Hauptziele in diesem Forschungsprojekt ist es daher, Offline- und Online-Lernstrategien zu nutzen, um relevante Computersimulationen mit relaxierten Sch?digungsmodellen zu erm?glichen. Darüber hinaus stellen neuartige Konvexifizierungssans?tze, die auf PDE-Formulierungen oder Polykonvexifizierung beruhen, vielversprechende Alternativen für relaxierte Modelle dar. Die mit diesen Ans?tzen verbesserte Effizienz und erwartbare Simulationsbeschleunigung wird für komplexere mechanische Probleme einschlie?lich spr?dem und duktilem Materialversagen im Sinne einer makroskopischen Rissausbreitung erforderlich sein, bei denen Lernstrategien alleine an ihre Grenzen sto?en. Daher ist das letzte Hauptziel dieses Forschungsprojekts, die inkrementellen Variationsformulierungen so zu erweitern, dass plastische Effekte in Kombination mit Sch?digung für spr?de und duktile Bruchprobleme erfassbar werden.

?

Projekt-Partner: Prof. Dr. Malte A. Peter (Universit?t Augsburg)

Projekt-Partner: Prof. Dr.-Ing. habil. Daniel Balzani (Ruhr Universit?t Bochum)

Projekt-Website

?

Autonome Forschung zur Exploration von Struktur-Eigenschafts-Beziehungen und Optimierung von Mikrostrukturen

PI: Prof. Dr. Daniel Peterseim

?

Die Entwicklung neuer Materialien spielt eine wichtige Rolle für technologische Innovationen. Im Zentrum des Interesses steht dabei der Zusammenhang zwischen den Prozessparametern, der lokalen Materialstruktur und den resultierenden Eigenschaften. Da der lokale Aufbau der Materialien ihre Eigenschaften wesentlich diktiert, sind die Bereitstellung und das Verst?ndnis von Struktur-Eigenschafts-Beziehungen (SEB) von gro?er Bedeutung. Das Projekt verfolgt das Ziel, zuverl?ssige SEB schnell und kostengünstig aufzustellen und damit realistische, herstellbare Materialstrukturen mit optimalen Eigenschaften zu identifizieren.
Die experimentelle Exploration der SEB verursacht einen erheblichen technologischen Aufwand. Die erreichbare begrenzte Datengrundlage stellt ein gro?es Hindernis für die Anwendung moderner Methoden des Maschinellen Lernens dar. Modellbasierte numerische Simulationen schaffen hier in Form synthetischer Daten Abhilfe. Ein praktisch relevanter Algorithmus erfordert darüber hinaus die automatisierte Generierung synthetischer Mikrostrukturen und die Durchführung numerischer Simulationen an ausgew?hlten Stichproben, um die experimentelle Datengrundlage gezielt zu erweitern. Dieses als autonome Forschung bezeichnete Verfahren wird in vier Schritten materialunabh?ngig entwickelt, implementiert und validiert. Insgesamt verspricht die Synthese von modellbasierter numerischer Simulation und datengetriebenen Algorithmen ein tieferes Verst?ndnis der Wirkmechanismen, die den SEB zugrunde liegen, sowie eine Beschleunigung der Materialentwicklung.

?

Projekt-Partner: Prof. Dr.-Ing. habil. Markus K?stner (TU Dresden)

?

Entkoppelnde numerische Methoden h?herer Ordnung für poroelastische Netzwerke

PI: Dr. Robert Altmann

?

Poroelastische Gleichungen spielen eine zentrale Rolle in zahlreichen Anwendungsfeldern wie der Geomechanik oder der Biomedizin. Das dazugeh?rige Modell wird beschrieben durch ein gekoppeltes System elliptisch-parabolischer Differentialgleichungen, welches gerade im drei-dimensionalen Fall sehr rechenintensiv ist. Die direkte Anwendung von Standardmethoden bildet daher selbst für moderne Rechner eine gro?e Herausforderung. Dieses Projekt hat das Ziel, neuartige und hoch effiziente Zeitdiskretisierungsverfahren h?herer Ordnung zu entwickeln und somit die numerische Approximation zu erleichtern. Dabei soll die Einfachheit monolithischer Ans?tze mit der Geschwindigkeit iterativer Verfahren, die das Problem in den elliptischen und parabolischen Teil entkoppeln, kombiniert werden. Da die Ortsdiskretizierung poroelastischer Gleichungen auf eine Differential-Algebraische Gleichung führt, stellt die erforderliche Konvergenzanalyse ein herausforderndes Unternehmen dar. Die neu entwickelten Verfahren sind semi-explizit und erweitern einen kürzlich vorgestellten Ansatz. Die Konvergenzanalyse basiert auf der Interpretation der semi-expliziten Diskretisierung als implizite Diskretisierung einer verwandten Gleichung mit zeitverz?gertem Term.

?

Projektpartner: Dr. Benjamin Unger (U Stuttgart)

?

?

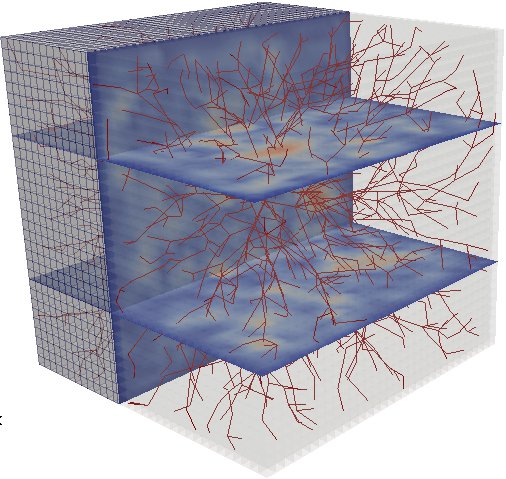
Numerische Multiskalenmethoden zur inversen Sch?tzung der effektiven Eigenschaften poroelastischer Gewebe

PI: Prof. Dr. Daniel Peterseim

?

Die Magnetresonanz-Elastographie (MRE) ist ein medizinisches Bildgebungsverfahren zur Identifizierung mechanischer Gewebsver?nderungen durch die Messung der Ausbreitung von Scher-und Kompressionswellen. Diese Technik kann nicht-invasiv und in vivo zur Diagnose und ?berwachung von Gewebeerkrankungen
wie Krebs und Fibrose eingesetzt werden. Leider sind Elastographiedaten nur auf einer relativ groben r?umlichen Skala (in der Gr??enordnung von Millimetern) verfügbar. In vielen Anwendungen ist man jedoch an
mikrostrukturellen Eigenschaften des Gewebes oder dem interstitiellen Gewebedruck interessiert. Um die nicht-invasive Diagnostik in diesem Bereich voran zu bringen, entwickelt das Projekt neuartige von MRE-Daten getriebene, mathematische und rechnergestützte Modelle zur Charakterisierung mehrskaliger Eigenschaften von biphasischen/vaskularisierten Weichgeweben. Die enge Zusammenarbeit mit den radiologischen Abteilungen der
Charite-Universit?tsmedizin Berlin und des Universit?tsklinikums Augsburg erm?glicht die Validierung der entwickelten Modelle um die angestrebte klinische Relevanz des Projekts zu gew?hrleisten.

?

Projektpartner: Dr. Alfonso Caiazzo (WIAS Berlin)

?

Externe Partner: Charite-Universit?tsmedizin Berlin/Universit?tsklinikum Augsburg

?

Konvexifizierte Variationsformulierungen bei gro?en Deformationen basierend auf homogenisierten, gesch?digten Mikrostrukturen

PI: Prof. Dr. Daniel Peterseim

?

Viele weiche Materialien wie Elastomere, verst?rkte Polymere und weiches biologisches Gewebe zeigen unter gro?en Verformungen anisotrope Entfestigungseffekte. Neben komplexer Spannungs-Dehnungs-Hysterese bei zyklischer Belastung, die mit Spannungs-Entfestigung einhergehen, ist signifikante Dehnungs-Entfestigung im Sinne von kleiner werdenden Spannungen bei steigender Dehnung ein wesentlicher Effekt in aktuellen Fragestellungen des Materialdesigns. Wesentliche Beispiele sind die Delamination oder der Faserauszug in verst?rkten Materialien. Die Entfestigungseffekte haben ihren Ursprung in einer Nukleation und Entwicklung von Hohlr?umen auf der Mikroskala, die gesch?digte Mikrostrukturen darstellen. Das resultierende makroskopische Verhalten kann im Rahmen klassischer Sch?digungs-Kontinuumstheorie ph?nomenologisch durch interne Variablen dargestellt werden, die den reduzierten Materialquerschnitt abbilden. Ab einer bestimmten St?rke der mikrokopischen Sch?digung werden die zugeh?rigen inkrementellen Modelle allerdings nicht-konvex, was wesentliche Probleme in der Verwendbarkeit und insbesondere in der numerischen Auswertung mit sich bringt.

Der Fokus dieses Forschungsprojekts ist die Aufstellung und Implementierung neuer konvexifizierter inkrementeller Variationsformulierungen, die a priori numerisch stabil sind. Die Konvexifizierungen nutzen homogenisierte Materialbeschreibungen der mikroskopischen Sch?digungsph?nomene. Der Konvexifizierungsprozess erlaubt eine direkte Interpretation als Evolution von Sch?digung der Mikrostruktur und die Modelle sind automatisch numerisch gutmütig, z.B. erlauben sie gitterunabh?ngige L?sungen. Die Hauptziele sind die Berücksichtigung von Dehnungs-Entfestigungs-Effekten im variationellen Sch?digungsmodell.

?

Projekt-Partner: Prof. Dr. Malte A. Peter (Universit?t Augsburg)

Projekt-Partner: Prof. Dr.-Ing. habil. Daniel Balzani (Ruhr Universit?t Bochum)

Projekt-Website

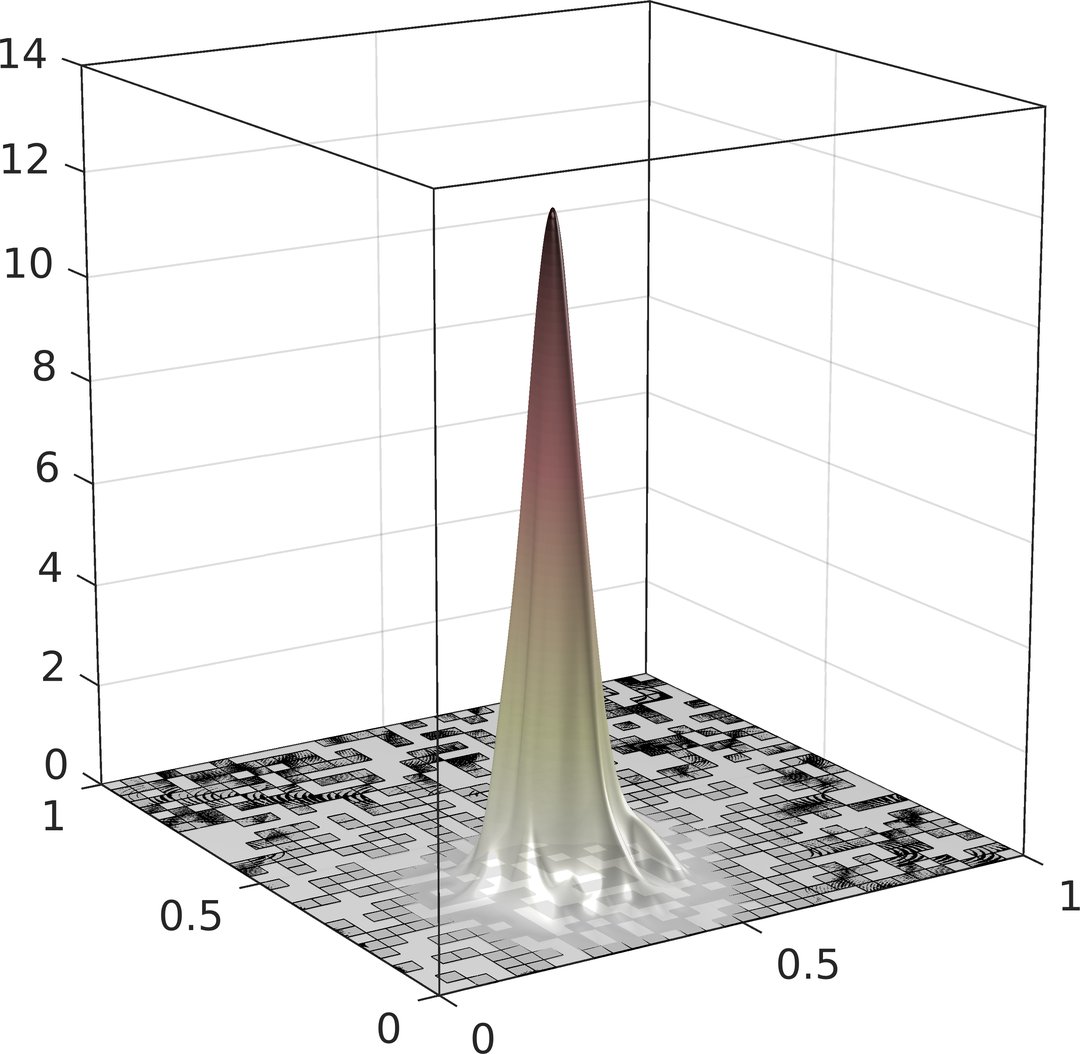
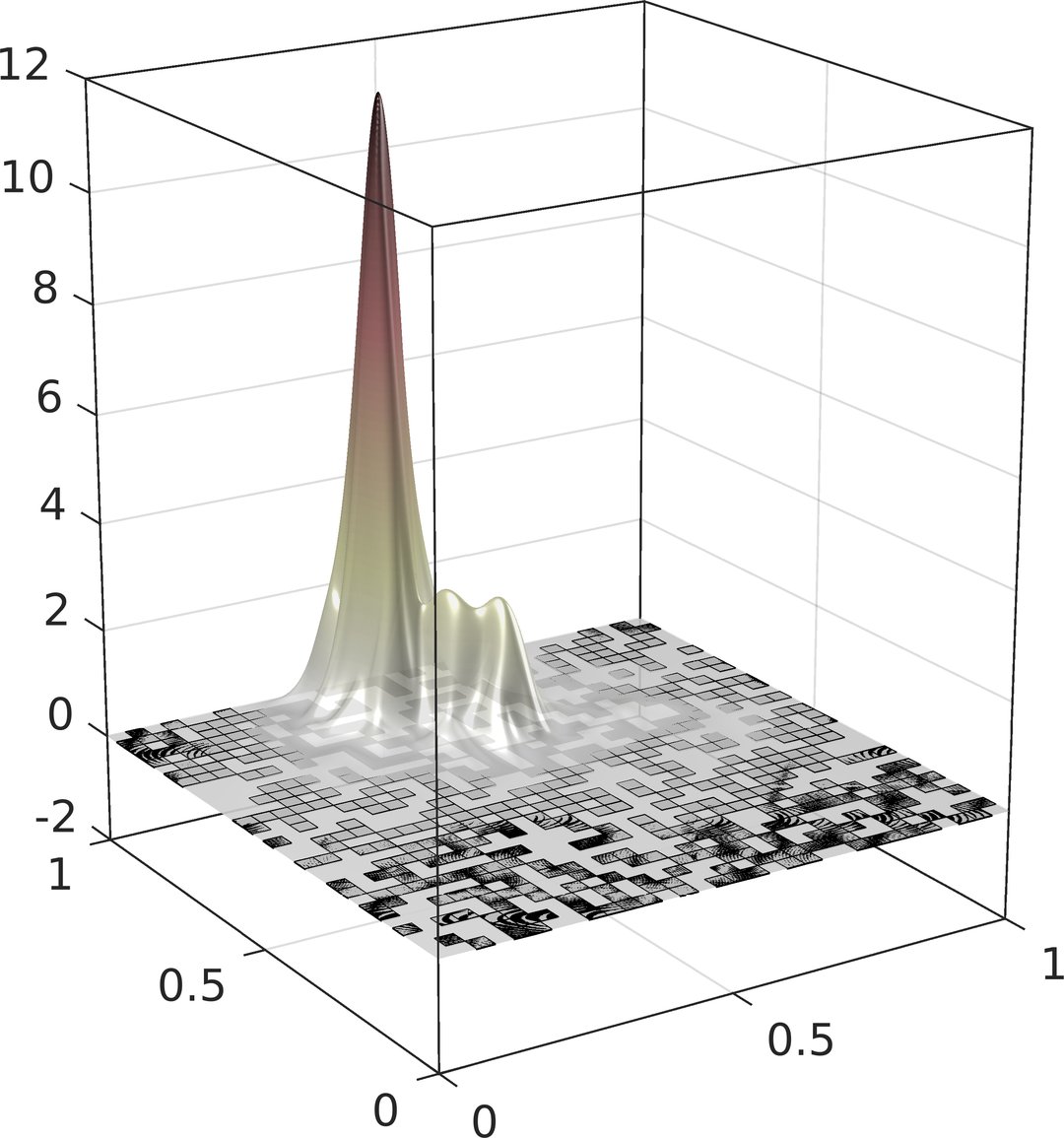
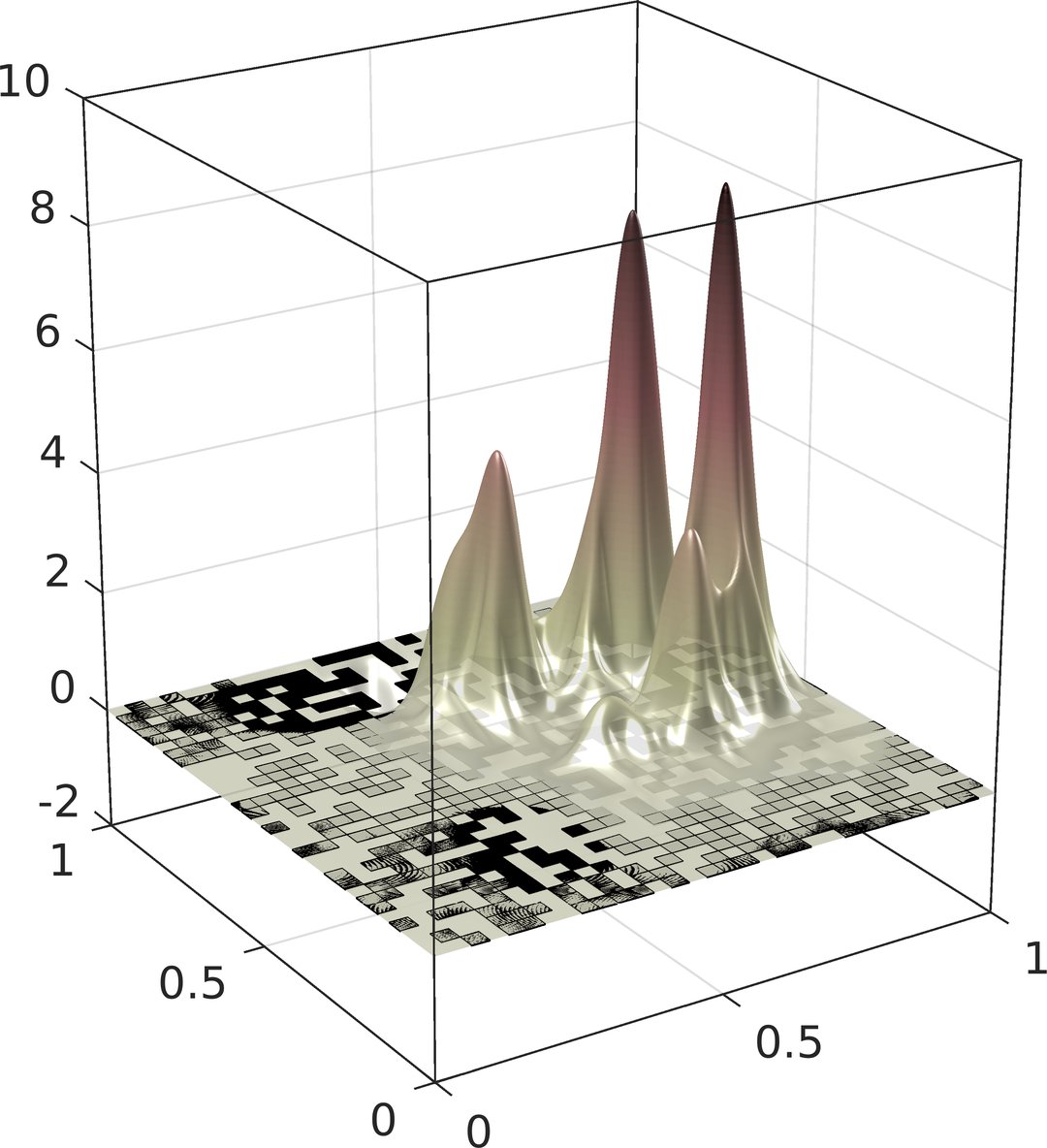
Computational Random Multiscale Problems

PI: Prof. Dr. Daniel Peterseim

?

Computersimulationen spielen l?ngst eine zentrale Rolle für den wissenschaftlichen und technologischen Fortschritt. Sie sind nicht nur die Grundlage für die Weiterentwicklung von Hochleistungsmaterialien (wie bsw. Faserverbundwerkstoffe, die? herk?mmliche Werkstoffe wie Stahl oder Aluminium in weiten Teilen der Produktentwicklung ersetzen), sie gestatten auch die Erkundung neuer physikalischer Ph?nomene für Hightech-Produkte der Zukunft, die experimentell bisher nur schwer zug?nglich sind (bsw. eigentümliche Aggregatzust?nde wie Bose-Einstein-Kondensate mit Anwendungen in futuristischen Technologien wie Atomlasern oder Quantencomputern). Allerdings sind die der Simulation zu Grunde liegenden mathematischen Modelle, wie auch die physikalischen Prozesse selbst, durch komplexe Effekte auf einer Vielzahl von L?ngen- und Zeitskalen gekennzeichnet. Der Versuch, diese inh?rente Mehrskaligkeit in Standard-Computermodellen abzubilden, führt selbst modernste Supercomputer an ihre Grenzen. Die Simulation solcher Ph?nomene erfordert daher eine neue Generation von Algorithmen (sogenannter numerischer Mehrskalenmethoden), die mit hierarchischen und adaptiven L?sungsstrategien die komplexen mathematischen Modelle auf ein berechenbares und wirtschaftliches Ma? reduzieren, ohne ihre Aussagekraft wesentlich zu beeintr?chtigen.

Das Projekt Computational Random Multiscale Problems widmet sich dem Design solcher Algorithmen/Mehrskalenmethoden und ihrer mathematischen Erforschung. Zu den Zielen z?hlen beispielsweise die Entwicklung effizienter und zuverl?ssiger Simulationsmethoden für Wellenph?nomene und Quantenphasenüberg?nge in zuf?lligen und ungeordneten Medien, sowie die Beantwortung damit einhergehender fundamentaler mathematischer und algorithmischer Fragen an den Schnittstellen von Numerischer Mathematik, Unsicherheitsquantifizierung und Numerischer Physik.

?

Informationsdienst der Gemeinschaft für Forschung und Entwicklung (CORDIS) der Europ?ischen Kommission

Entkoppelte numerische Methoden für nichtlineare parabolische Probleme mit dynamischen Randbedingungen

PI: Dr. Robert Altmann

?

Ziel des Projekts ist die Konstruktion, Analyse und Implementierung robuster numerischer Verfahren für nichtlineare parabolische Anfangswertprobleme mit dynamischen Randbedingungen. Solche Systeme treten in Anwendungen auf bei denen das Verhalten am Rand in besonderer Weise widergespiegelt werden muss. Grundlage für die Entwicklung neuer Verfahren ist die Umformulierung des Problems in Form einer partiell-differential-algebraischen Gleichung (PDAE). Dabei werden Gebiets- und Randdynamik zusammen als gekoppeltes System betrachtet, die mithilfe eines Lagrange Multiplikators verknüpft werden. Basierend auf so einer PDAE Formulierung ist es nun m?glich, numerisch robuste Diskretisierungsverfahren zu konstruieren. Für die Stabilit?t der Ortsdiskretisierung sind sogenannte gemischte Methoden n?tig, wohingegen für die Stabilit?t in der Zeit bekannte Techniken aus dem Bereich differential- algebraischer Gleichungen angewandt werden. Im Gegensatz zur ursprünglichen Problemformulierung wird die Kopplung aus Gebiets- und Randdynamik hier nicht im Ansatzraum integriert sondern in Form einer zus?tzlichen Systemgleichung explizit erzwungen. Diese formale Entkopplung bietet zus?tzliche Freiheiten bei der Wahl der Ansatzr?ume für die Ortsdiskretisierung. Insbesondere k?nnen die Triangulierungen des Gebiets und des Randes unabh?ngig gew?hlt werden, was gerade bei heterogenen Problemen Vorteile bietet. Das zweite Ziel des Projekts ist die Entwicklung von Splitting Verfahren für den numerischen Umgang mit auftretenden Nichtlinearit?ten sowie der Entkopplung von Gebiets- und Randdynamik.

?

Adaptive isogeometrische Modellierung von Diskontinuit?ten in komplex berandeten heterogenen Festk?rpern

PI: Prof. Dr. Daniel Peterseim

?

Bei der Entwicklung innovativer Produkte kommen neuartige Leichtbaustrukturen mit einer ausgepr?gten Mikrostruktur zum Einsatz. Die zuverl?ssige rechnerische Auslegung dieser Komponenten erfordert das physikalische Verst?ndnis und vor allem die numerische Modellierung von Rissph?nomenen. Simulationstechniken müssen dabei sowohl das Versagen von Grenzfl?chen und einzelnen Materialphasen sowie deren Zusammenspiel berücksichtigen. Darüber hinaus muss die dreidimensionale Natur des Problems erfasst werden, um realistische Vorhersagen des Materialverhaltens auf der Basis von Simulationen zu erm?glichen. Zu diesem Zweck entwickeln wir neue numerische Modelle und Methoden auf der Grundlage adaptiver Spline-basierter Diskretisierungsverfahren der Isogeometrischen Analysis (IGA) sowie von Phasenfeldmodellen des Rissfortschritts. Die Hauptziele des Projekts stehen in engem Zusammenhang mit zentralen Herausforderungen an der Schnittstelle von Numerischer Mathematik und Mechanik. Hierzu z?hlen die Darstellung und adaptive Verfeinerung unstrukturierter Spline-Oberf?chen, die Kopplung solcher Spline-Fl?chen mit strukturierten Volumengittern, die Regularisierung heterogener Materialien sowie die rigorose mathematische Fehleranalyse und -kontrolle in relevanten Diskretisierungsregimen.

?

Projekt-Partner: Prof. Dr.-Ing. habil. Markus K?stner (TU Dresden)

Projekt-Webseite

?